РАССТОЯНИЕ.
- АВС- правильный треугольник, О его центр ОМ- перпендикуляр к плоскости АВС, ОМ=1.
Сторона треугольника равна 3. Найдите расстояние от точки М до вершин треугольника.
- АВСД - квадрат со стороной, равной
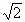 ,
О - точка пересечение его диагоналей, ОЕ-
перпендикуляр к плоскости АВС, ОЕ =
,
О - точка пересечение его диагоналей, ОЕ-
перпендикуляр к плоскости АВС, ОЕ = 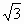 .
Найдите расстояние от точки Е до вершин квадрата.
.
Найдите расстояние от точки Е до вершин квадрата.
- Отрезок АВ не пересекает плоскость a
, АС^a и ВД^a,
АС=20, ВД=30, МОАВ, причем АМ :
МВ = 2 : 3, ММ1^a
. Найдите ММ1.
- Отрезок АВ пересекает плоскость a
, АС^a и ВД^a,
АС=14, ВД=10, Е- середина АВ, ЕЕ1^a
. Найдите ЕЕ1.
- Через вершину А треугольника АВС
проведена плоскость a ,
параллельная ВС, ВВ1^a
и СС1^a ,
СС1=4, АС=
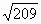 ,
АВ1=
,
АВ1= ,
РВАС=60º. Найдите ВС.
,
РВАС=60º. Найдите ВС.
- Через вершину Е треугольника ЕРМ
проведена плоскость a ,
параллельная РМ, ММ1^a,
ММ1=12см, К- точка
пересечения медиан треугольника, и КК1^a.
Найдите КК1.



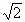 ,
О - точка пересечение его диагоналей, ОЕ-
перпендикуляр к плоскости АВС, ОЕ =
,
О - точка пересечение его диагоналей, ОЕ-
перпендикуляр к плоскости АВС, ОЕ = 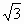 .
Найдите расстояние от точки Е до вершин квадрата.
.
Найдите расстояние от точки Е до вершин квадрата.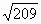 ,
АВ1=
,
АВ1= ,
РВАС=60º. Найдите ВС.
,
РВАС=60º. Найдите ВС.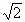 ,
О - точка пересечение его диагоналей, ОЕ-
перпендикуляр к плоскости АВС, ОЕ =
,
О - точка пересечение его диагоналей, ОЕ-
перпендикуляр к плоскости АВС, ОЕ = 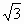 .
Найдите расстояние от точки Е до вершин квадрата.
.
Найдите расстояние от точки Е до вершин квадрата.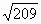 ,
АВ1=
,
АВ1= ,
РВАС=60º. Найдите ВС.
,
РВАС=60º. Найдите ВС.