ПРЯМАЯ, ПАРАЛЛЕЛЬНАЯ ПЛОСКОСТИ.

1. Из внешней точки А проведен к плоскости М отрезок АВ. Он разделен точкой С в отношении 3:4 (от А к В), и через нее проведен параллельно плоскости М отрезок СД=12см. Через точку Д проведен к плоскости М отрезок АДЕ. Определите расстояние между точками В и Е.
2. АВ и СД- параллельные отрезки, лежащие в двух пересекающихся плоскостях; АЕ и ДК- перпендикуляры на линию пересечения плоскостей. Расстояние АД=5см и отрезок ЕК= 4см. Найти расстояние между прямыми АВ и СД.
3. В параллелограмме АВСД вершины А и Д находятся на плоскости М, а В и С- вне ее. Сторона АД=10см, сторона АВ=15см, проекции диагоналей АС и ВД на плоскость М соответственно равны 13,5 см и 10,5см. Определите диагонали.
4. Через одну из сторон ромба проведена плоскость на расстоянии 4см от противолежащей стороны. Проекции диагоналей ромба на эту плоскость равны 8см и 2см. Найти проекции сторон.
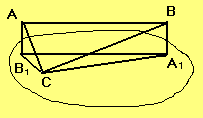
5. Через вершину прямого угла С прямоугольного треугольника АВС проведена плоскость параллельно гипотенузе на расстоянии 1дм от нее. Проекции катетов на эту плоскость равны 3дм и 5дм. Определить проекцию гипотенузы на эту же плоскость. (см рис)
6. АВ - отрезок, параллельный плоскости М; АС и ВД - две равные наклонные к плоскости М, проведенные перпендикулярно к отрезку АВ и разных направлениях от него. Отрезок АВ, равный 2см, отстоит от плоскости М на 7см, а отрезки АС и ВД содержат по 8см. Определить расстояние СД.